Elektrotechnische Grundlagen
Grundlegende Größen
Spannung (U)
Die Spannung wird als Größe mit einem \(U\) bezeichnet und wird üblicherweise in der Einheit \(V\) (Volt) angegeben. Sie ist, vereinfacht gesagt, ein Maß dafür, wie groß der Energieunterschied der Elektronen zwischen den jeweiligen Polen ist. Beispiele für geläufige Spannungswerte wären z.B. \(12V\) für eine Autobatterie oder \(230V\) die an einer Steckdose anliegen. Misst man eine Spannung zwischen zwei Punkten, so spricht man davon, dass die Spannung zwischen diesen beiden Punkten "abfällt".
Strom (I)
Der Strom wird als Größe mit einem \(I\) bezeichnet und wird üblicherweise in der Einheit \(A\) (Ampere) angegeben. Er ist ein Maß dafür, wie viele Elektronen in einer bestimmten Zeit einen bestimmten Punkt durchqueren.
Widerstand (R)
Der elektrische Widerstand wird als Größe mit einem \(R\) bezeichnet und wird üblicherweise in der Einheit "Ohm" angegeben. Der elektrische Widerstand gibt an, welche Spannung an einem Verbraucher bei einer definierten Stromstärke abfällt.
Die drei Größen hängen über die Formel \(U = R * I\) zusammen. Diese kann beliebig nach den einzelnen Größen umgestellt werden \((R = U/I, I = U/R)\).
Kapazität (C)
Im Bereich der Akkutechnik spricht man von Kapazität, wenn man ausdrücken will wie viel Ladung in einem Akku gespeichert werden kann. Sie wird in der Einheit \(Ah\) angegeben und gibt somit an, wie lange man einen bestimmten Strom aus einem Akku/einer Zelle entnehmen kann. Der Zusammenhang lautet: \(C = I * t\). Bsp.: Aus einem Akku mit der Kapazität 10Ah kann man einem Strom von \(1A\) für Stunden entnehmen .
Leistung (P)
Die Leistung eines elektrischen Verbrauchers/einer elektrischen Quelle wird mit dem Produkt aus Spannung und Strom berechnet: \(P = U * I\) oder auch \(P = R * I^2\). Die übliche Einheit ist \(W\) (Watt). Bei einem Motor z.B. wäre die maximale Leistung ein Indikator dafür, welche "Kraft" er maximal innerhalb der Betriebsspezifikationen entwickeln kann.
Energie/Arbeit (W)
Die Energie wird mit einem \(E\) oder \(W\) bezeichnet und wird üblicherweise in \(Wh\) (Wattstunden) oder auch \(kWh\) (Kilowattstunden) angegeben. Die Energie hängt mit der Leistung wie folgt zusammen: \(E = P * t\). Wird beispielsweise ein Motor mit seiner Maximalleistung von \(250W\) für eine Stunde \((1h)\) betrieben, so wandelt er \(250W * 1h = 250Wh = 0,25kWh\) elektrische Energie um.
Serien-/Parallelschaltung
Grundsätzlich gibt es zwei Möglichkeiten bei der Verschaltung zweier oder mehrerer Bauteile:
Serienschaltung
Dabei werden die Bauteile direkt hintereinander verbunden; gewissermaßen korrespondiert dann der "Ausgang" des ersten Bauteils mit dem "Eingang" des zweiten usw. Bei dieser Art der Verschaltung fließt durch alle Bauteile hintereinander immer der gleiche Strom, während sich die Gesamtspannung auf die einzelnen Bauteile verteilt. Die Einzelspannung eines bestimmten Elements \(x\) ergibt sich wie folgt: \(U(x) = U_{Ges} / R_{Ges.} * R(x)\). Da sich bei dieser Art der Verschaltung die Einzelspannungen addieren, eignet sie sich um durch Serienverschaltung einzelner Zellen eine höhere Gesamtspannung zu erzielen.
Parallelschaltung
Hierbei werden die Bauteile jeweils gleichartig verbunden. Der "Eingang" des ersten Bauteils fällt gewissermaßen mit dem "Eingang" des zweiten Bauteils zusammen usw. Bei dieser Verschaltung liegt an allen Bauteilen/Elementen die gleiche Spannung an, jedoch teilt sich der Gesamtstrom auf die einzelnen "Äste" der Verschaltung auf. Dadurch steigt bei der Verschaltung von Zellen der maximal mögliche Gesamtstrom und die entnehmbare Kapazität.
Kombination von Serienschaltung und Parallelschaltung
Auch die Kombination der beiden Verschaltungsarten ist möglich. Um z.B. einen Akku mit der Spannung \(36V\) und der Kapazität \(5Ah\) aus Einzelzellen mit einer Spannung von \(3,6V\) und einer Kapazität von jeweils \(1Ah\) herzustellen, muss man zehn mal jeweils fünf Einzelzellen parallel verschalten und anschließend die entstandenen zehn Zellenblöcke seriell verschalten. Somit ergibt sich eine Spannung von \(10 * 3,6V = 36V\) und eine Kapazität von \(5 * 1Ah = 5Ah\).
Lithiumakku-Grundlagen
Spannung
Die Spannung eines Lithiumakkus wird in der Einheit \(V\) (Volt) angegeben. Es muss unterschieden werden zwischen der Nominalspannung, Entladeschlussspannung und Ladeschlussspannung.
Nominalspannung
Die Nominalspannung eines Akkus ergibt sich aus der Anzahl der seriell verschalteten Zellen und deren Nominalspannung. Diese haben wir für einige Zellentypen dargestellt:
Li-Ion: \(3,6V\)
LiFePO4: \(3,3V\)
LiPo: \(3,7V\)
Die Ladeschlussspannung liegt stets deutlich über der Nominalspannung, die Entladeschlussspannung deutlich darunter. Im Verlauf des Entladevorgangs sinkt die Spannung von der anfänglichen Ladeschlussspannung über die Nominalspannung bis auf die Entladeschlussspannung.
Entladeschlussspannung
Lithiumakkus dürfen nicht unter ein bestimmtes Spannungslevel entladen werden. Passiert dies doch, schädigt das die Lebensdauer immens. Zusätzlich kann durch eine Tiefentladung (Entladung unter Entladeschlussspannungsniveau) kaum zusätzliche Kapazität genutzt werden. Aus diesem Grund sollten Lithiumakkus niemals unter die Entladeschlussspannung entladen werden. Ein BMS oder Unterspannungsschutz übernimmt diese Funktion.
Die Werte lauten wie folgt für verschiedene Zellentypen (es können hierzu Abweichungen auftreten, die genauen Werte können Sie aus dem Datenblatt des jeweiligen Zellenherstellers entnehmen):
Li-Ion: \(3,0V\)
LiFePO4: \(2,0V\)
LiPo: \(3,0V\)
Ladeschlussspannung
Lithiumakkus dürfen nur auf ein bestimmtes Spannungsniveau geladen werden, da sie ansonsten irreparabel zerstört werden. Daher ist es erforderlich, dass das Ladegerät auf den exakt notwendigen Wert eingestellt wird, um eine Überladung zu verhindern. Zusätzlich sollte ein Überspannungsschutz verwendet werden (bereits Bestandteil unserer BMS) um bei einem Defekt des Ladegeräts oder Anschluss eines falschen Ladegeräts den Akku nicht zu beschädigen.
Kapazität
Die Kapazität eines Akkus wird in Ah (Amperestunden) angegeben und gibt Aufschluss darüber, wie lange der Akku einen bestimmten Strom liefern kann bis er leer ist. Beispiel: Es kann Stunden \((h)\) lang ein Strom von \(1A\) entladen werden. Ebenso kann \(0,5h\) (\(30min\)) lang ein Strom von \(20A\) entnommen werden.
Akkupackkonfiguration
Eine Zelle ist die kleinste Einheit eines Akkupacks. Da diese für die meisten Anwendungen eine zu kleine Spannung und/oder Kapazität besitzt, wird sie oftmals mit weiteren Zellen verbunden um den Anforderungen gerecht zu werden. Um die Spannung zu erhöhen, werden Zellen seriell verschaltet:
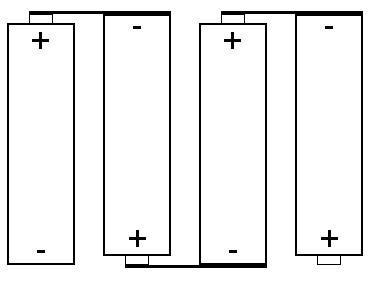
Bei dieser Verschaltung muss darauf geachtet werden, dass die einzelnen Zellen bei Ladeende die selbe Spannung haben. Die Anzahl der seriell verschalteten Zellen wird mit dem Suffix \(s\) dargestellt, z.B. 3s (drei Zellen seriell), 10s (…) Die Nominalspannung des Akkus ergibt sich aus der Nominalspannung der Einzelzelle multipliziert mit der Anzahl der seriell verschalteten Einzelzellen.
Eine parallele Verschaltung ergibt mehr Kapazität:
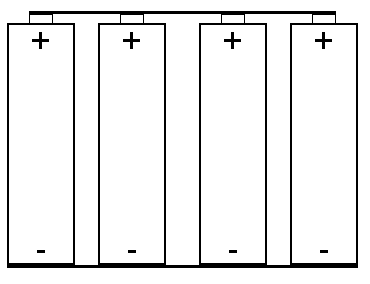
Bei dieser Verschaltung haben alle Zellen stets die gleiche Spannung, da sie sich durch die Parallelschaltung immer angleichen. Die Anzahl der parallel verschalteten Zellen wird mit dem Suffix p dargestellt: 2p (zwei Zellen parallel), 8p (acht Zellen parallel)… Die Nominalkapazität eines Akkus ergibt sich aus der Kapazität der Einzelzelle multipliziert mit der Anzahl der parallel verschalteten Zellen.
Werden sowohl seriell als auch parallel verschaltete Zellen zu einem Akkupack konfektioniert, so ergeben sich veränderte Spannungen und Kapazitäten, z.B.:
10s5p (aus Einzelzellen mit jeweils nominal \((3,6V)/(2Ah) = 10 * 3,6V\) und \(5 * 2Ah = (36V)/(10Ah)\)
"C"-Rating
Mit dem C Rating wird der maximale Entladestrom und/oder Ladestrom angegeben. Man multipliziert den C Wert mit der Kapazität und bekommt als Ergebnis den maximalen Strom in \(A\).
Bsp.: Bei einem \(10Ah\) Akku mit einem C-Rating (für Lade- und Entladestrom) von \(2C\) ergibt sich ein maximaler Lade-/Entladestrom von \(20A\).
Innenwiderstand eines Akkus
Elektrotechnisch gesehen besitzt jedes elektronische Bauelement einen sog. "Innenwiderstand", so auch ein Lithiumakku. Der Innenwiderstand ist ein Maß dafür, wie viel (Heiz-)Leistung an einem Akku beim Entladen abfällt.Je höher der Widerstand ist, desto größer die Erwärmung der Zelle beim Entladen. Theoretisch erwünschte niedrige Innenwiderstände gehen allerdings oft einher mit einer geringeren Energiedichte. Man kann sich einen realen Akku als ideale Spannungsquelle (kein Spannungsabfall unter Last) und einem seriell verschalteten Widerstand (Entspricht dem Innenwiderstand) vorstellen:
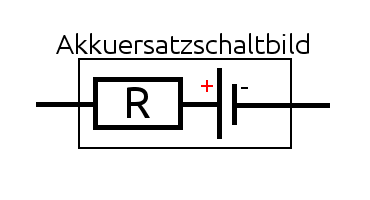
Die Spannung die man an einem Akku im Leerlauf (ohne Belastung) messen kann, nennt man Leerlaufspannung. Sobald der Akku belastet wird, fällt die Leerlaufspannung auf die Belastungsspannung ab. Beispiel: Verwendet man einen \(36V\) Fahrradakku mit einem Innenwiderstand von \(0,1Ω\) an einem \(3,5Ω\) Verbraucher (entspricht grob einem \(250W\) Antrieb bei Volllast), ergibt sich folgender Stromfluss:
\(I = U/R = 36V/(3,5 + 0,1)= 10A\)
Leistung: \(P = U * I = 36V * 10A = 360W\)
An unserem Verbraucher liegen von den \(36V\) allerdings nur noch \(U = R * I = 3,5Ω * 10A = 35V\) an. \(U = R * I = 0,1Ω * 10A = 1V\) fallen am Innenwiderstand ab. Deshalb ist aus einem Akku niemals die nominale Anzahl an Wattstunden zu entnehmen. Ein Teil wird immer in Wärme umgewandelt und erhitzt den Akkupack.
Bei einer Serienschaltung von Zellen addieren sich die Widerstände: \(R_(Gesamt) = R_1 + R_2 + R_3 + ... + R_i\) Bei einer Parallelschaltung verkleinern sich die Widerstände: \(1/R_(Gesamt) = 1/R_1 + 1/R_2 + ... + 1/R_i\)
Ich sehe die Zahl "18650" erstaunlich oft, was bedeutet sie?
Diese Zahl stellt ein standardisiertes Zellenformat dar: \(18mm\) Durchmesser bei \(65mm\) Höhe. Die ersten zwei Ziffern nennen den Durchmesser (in \(mm\)), die dritte, vierte und fünfte Stelle ergeben die Länge (in \(1/10mm\)).